Booil Jung

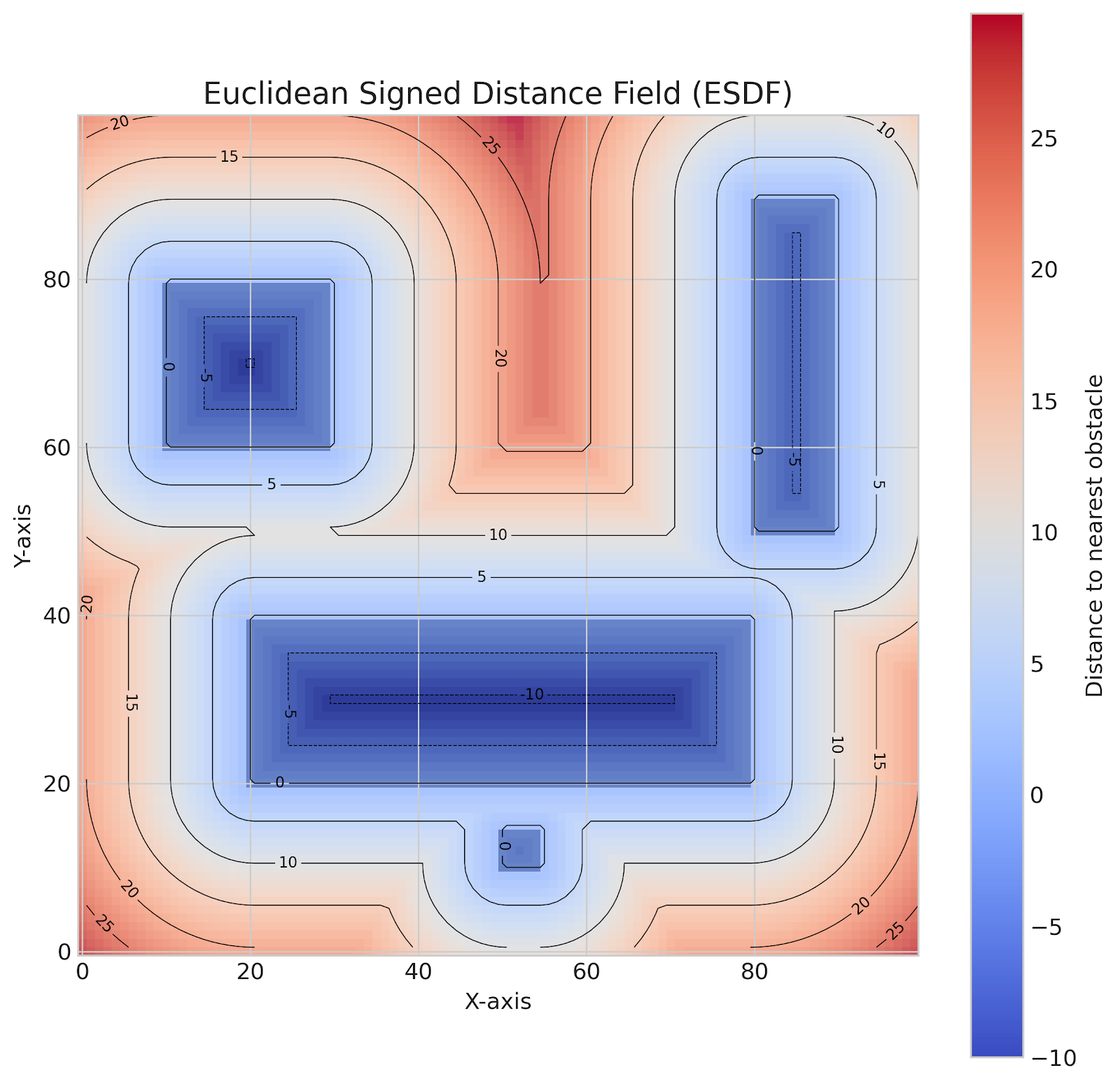
ESDF (Euclidean Signed Distance Field)

컴퓨터 그래픽스, 컴퓨터 비전, 그리고 로보틱스 분야의 발전은 3차원 공간과 그 안에 존재하는 객체를 어떻게 효율적이고 정확하게 디지털 데이터로 표현하는가에 대한 근본적인 질문과 함께해왔다.1 전통적으로 3D 형상을 표현하는 주류 방식은 명시적(explicit) 표현이었다. 이는 객체의 표면을 직접적으로 기술하는 방식으로, 가장 대표적인 예로는 다각형 메시(polygonal mesh)와 포인트 클라우드(point cloud)가 있다. 다각형 메시는 정점(vertex), 간선(edge), 면(face)의 집합으로 표면을 구성하며, 렌더링 파이프라인에 친화적이라는 장점 때문에 오랫동안 표준으로 사용되어 왔다. 포인트 클라우드는 LiDAR나 깊이 카메라와 같은 3D 스캐닝 장비로부터 직접 얻어지는 3D 점들의 집합으로, 원시 데이터(raw data)를 그대로 표현하는 가장 단순한 형태이다.3

그러나 이러한 명시적 표현 방식들은 본질적인 한계를 가진다. 첫째, 위상(topology) 변화에 취약하다. 예를 들어, 두 객체가 합쳐지거나 하나의 객체가 쪼개지는 현상을 메시 구조로 표현하려면 복잡한 재메싱(remeshing) 과정이 필요하다. 둘째, 불완전한 데이터 처리가 어렵다. 실제 센서로부터 얻어진 포인트 클라우드는 구멍(hole), 노이즈(noise), 불균일한 밀도 등 다양한 결함을 포함하는데, 이러한 데이터로부터 온전하고 닫힌(watertight) 메시를 재구성하는 것은 매우 어려운 문제이다.1 또한, 표현의 정밀도가 정점이나 점의 개수에 직접적으로 의존하기 때문에, 고품질의 형상을 표현하기 위해서는 막대한 양의 데이터가 필요하다는 단점도 존재한다.

이러한 명시적 표현의 한계를 극복하기 위한 대안으로 암시적(implicit) 표현 방식이 부상하였다. 암시적 표현은 표면 자체를 직접 기술하는 대신, 공간상의 한 점이 주어진 형상의 내부에 있는지, 외부에 있는지, 혹은 표면 위에 있는지를 판별하는 함수 $f(x, y, z)$를 통해 기하를 간접적으로 정의한다.5 표면은 이 함수의 특정 등위 집합(level set), 예를 들어 $f(x,y,z)=0$을 만족하는 점들의 집합으로 정의된다.

이러한 접근 방식은 여러 강력한 장점을 제공한다. 첫째, 표현이 연속적(continuous)이다. 이산적인 점이나 면이 아닌 연속 함수로 공간 전체를 정의하기 때문에, 이론적으로 무한한 해상도를 가지며 이산화로 인한 계단 현상(aliasing)이 없다.8 둘째, 메모리 효율성이 높을 수 있다. 복잡한 형상이라도 상대적으로 적은 수의 파라미터를 가진 함수로 표현할 수 있기 때문이다. 셋째, 견고한 기하 연산이 가능하다. 두 형상의 합집합, 교집합, 차집합과 같은 구성적 입체 기하(Constructive Solid Geometry, CSG) 연산을 간단한 함수 연산으로 처리할 수 있으며, 위상 변화에 자연스럽게 대처할 수 있다.9

다양한 암시적 표현 중에서도 가장 널리 사용되고 강력한 도구가 바로 부호 거리 필드(Signed Distance Field, SDF)이다. SDF는 공간의 모든 점 x에 대해, 그 점에서 가장 가까운 표면까지의 거리를 값으로 가지고, 그 부호(sign)를 통해 점이 표면의 내부에 있는지 외부에 있는지를 나타내는 스칼라 필드(scalar field)이다.7 일반적으로 표면의 내부는 음수(SDF<0), 외부는 양수(SDF>0), 그리고 표면 자체는 0(SDF=0)으로 정의된다.5 이처럼 SDF는 단순한 점유(occupancy) 정보를 넘어, 표면까지의 ‘거리’라는 풍부한 메트릭 정보를 공간 전체에 걸쳐 제공한다.

본 보고서는 수많은 SDF 변형 중에서도 가장 기본적이면서도 중요한 유클리드 부호 거리 필드(Euclidean Signed Distance Field, ESDF)에 대한 심층적인 고찰을 목표로 한다. ESDF는 거리 측정의 기준으로 우리에게 가장 직관적인 유클리드 거리(Euclidean distance)를 사용한다. 보고서는 먼저 ESDF의 수학적 정의와 핵심적인 특성을 분석하고, 이어서 ESDF를 생성하는 다양한 고전적 및 최신 알고리즘들을 원리 중심으로 상세히 설명할 것이다. 다음으로 컴퓨터 그래픽스와 로보틱스라는 두 핵심 분야에서 ESDF가 어떻게 활용되어 혁신적인 기술들을 가능하게 했는지 구체적인 사례를 통해 분석한다. 마지막으로, TSDF(Truncated Signed Distance Field)와 같은 연관 표현 방식과의 비교를 통해 그 차이점과 장단점을 명확히 하고, 최근 3D 딥러닝의 부상과 함께 등장한 신경망 기반 SDF 패러다임의 최신 동향까지 아우르며 ESDF의 현재와 미래를 종합적으로 조망하고자 한다.

ESDF의 수학적 정의를 엄밀하게 내리기 위해서는 먼저 거리 공간(metric space)의 개념에서 출발해야 한다. 거리 공간 $(X, d)$가 주어졌을 때, 이 공간의 부분집합 Ω⊂X를 하나의 3D 형상으로 생각할 수 있다. 이때 ∂Ω는 형상 Ω의 경계(boundary), 즉 표면을 나타낸다.

공간상의 임의의 한 점 x∈X에서 집합 ∂Ω까지의 거리는 점 x와 ∂Ω에 속하는 모든 점 y 사이의 거리 d(x,y) 중 가장 작은 값으로 정의된다. 수학적으로 이는 하한(infimum)을 사용하여 다음과 같이 표현된다.7

\(d(x, \partial\Omega) = \inf_{y \in \partial\Omega} d(x, y)\) 여기서 inf는 집합의 가장 큰 하계(greatest lower bound)를 의미하며, 이는 최소값(minimum)이 존재하지 않을 수 있는 경우까지 포함하는 더 일반적인 개념이다. 유클리드 공간과 같은 완비 거리 공간(complete metric space)에서는 이 값이 항상 존재하며, 가장 가까운 점이 실제로 존재하므로 최소값과 동일하다.

이 거리 함수를 기반으로, 부호(sign)를 추가하여 부호 거리 함수(SDF) $f(x)$를 정의할 수 있다. 부호는 점 x가 형상 Ω의 내부에 있는지, 아니면 외부에 있는지에 따라 결정된다. 컴퓨터 그래픽스와 로보틱스 분야에서 널리 사용되는 일반적인 관례(convention)는 형상의 내부를 음수(-), 외부를 양수(+)로 정의하는 것이다.5 이 관례에 따른 ESDF의 공식적인 정의는 다음과 같다.7

\(f(x) = \begin{cases} d(x, \partial\Omega) & \text{if } x \in \Omega^c \\ 0 & \text{if } x \in \partial\Omega \\ -d(x, \partial\Omega) & \text{if } x \in \Omega \end{cases}\) 여기서 Ωc는 Ω의 여집합, 즉 형상의 외부를 의미한다. 이 정의에 따르면, ESDF의 값은 표면으로부터 멀어질수록 절댓값이 커지며, 부호를 통해 내/외부를 즉시 판별할 수 있다.

다만, 일부 문헌이나 응용에서는 내부를 양수, 외부를 음수로 정의하는 반대의 관례를 채택하기도 하므로 7, 특정 구현이나 논문을 참조할 때는 해당 문서에서 사용하는 부호 관례를 명확히 확인하는 것이 매우 중요하다.

ESDF는 단순한 거리 정보의 집합을 넘어, 응용에 매우 유용한 여러 가지 강력한 수학적 특성을 지닌다.

미분 가능성 (Differentiability)

만약 형상 Ω의 경계 ∂Ω가 조각적으로 매끄럽다면(piecewise smooth), ESDF 함수 $f(x)$는 경계를 제외한 거의 모든 곳에서(almost everywhere) 미분 가능하다.7 이는 ESDF가 제공하는 가장 강력하고 실용적인 장점 중 하나이다. 미분 가능성은 그래디언트(gradient)를 계산할 수 있음을 의미하며, 이는 후술할 표면 법선 벡터 계산이나 최적화 기반 알고리즘 적용의 근간이 된다.

아이코날 방정식 (Eikonal Equation)

ESDF의 그래디언트 벡터 ∇f의 크기(magnitude)는 경계를 제외한 모든 점에서 항상 1이다.

\(|\nabla f| = 1\) 이 식은 아이코날 방정식(Eikonal equation)으로 알려져 있으며, 빛이나 파동의 전파(wave propagation) 현상을 모델링하는 편미분 방정식이다.7 ESDF가 이 방정식을 만족한다는 사실은 거리 필드가 파면이 일정한 속도로 퍼져나가는 것과 유사한 성질을 가짐을 의미하며, 이는 Fast Marching Method와 같은 일부 ESDF 생성 알고리즘의 이론적 기반이 된다.

표면 법선 벡터 (Surface Normal Vector)

경계 ∂Ω 상의 한 점 x에서 ESDF의 그래디언트 $\nabla f(x)$는 그 점에서의 표면 법선 벡터(surface normal vector)와 방향이 같다. 앞서 정의한 관례(내부 음수, 외부 양수)에 따르면, 그래디언트는 거리가 증가하는 방향, 즉 표면의 외부를 향하므로 외향 법선 벡터(outward normal vector)가 된다. 만약 내향 법선 벡터 N이 필요하다면 그래디언트의 부호를 바꾸면 된다.7

\(N(x) = -\nabla f(x) \quad \text{for } x \in \partial\Omega\) 이 특성은 ESDF가 단순히 표면의 위치(f=0)뿐만 아니라 표면의 국소적인 방향 정보까지 암시적으로 인코딩하고 있음을 보여준다. 따라서 ESDF는 표면 법선 벡터 필드의 미분 가능한 확장(differentiable extension)으로 간주될 수 있다.7 이 법선 정보는 컴퓨터 그래픽스의 사실적인 렌더링을 위한 조명 계산이나 로보틱스에서 충돌 회피 방향을 결정하는 데 결정적인 역할을 한다.

ESDF의 ‘E’는 유클리드(Euclidean)를 의미하며, 이는 거리 측정의 기준으로 유클리드 거리 메트릭을 사용함을 명시한다. 그러나 실제 응용에서는 계산 효율성 등의 이유로 다른 거리 메트릭이 고려되기도 한다.

유클리드 거리 (L2 Norm)

유클리드 거리는 두 점 사이를 잇는 가장 짧은 직선 거리를 의미하며, 피타고라스 정리에 기반한다. 2차원 공간의 두 점 $p_1=(x_1, y_1)$과 p2=(x2,y2) 사이의 유클리드 거리는 다음과 같이 계산된다.12

\(d_{L2}(p_1, p_2) = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\) 이는 우리가 일상적으로 인식하는 ‘거리’와 가장 일치하는 기하학적으로 직관적이고 정확한 측정 방식이다. 따라서 ESDF는 가장 자연스러운 형태의 거리 필드를 생성한다.14

맨해튼 거리 (L1 Norm, Taxicab Geometry)

맨해튼 거리는 격자 형태의 도시에서 길을 따라 이동하는 것처럼, 각 좌표축을 따라서만 이동할 때의 거리 합으로 정의된다. 일명 택시 거리(taxicab geometry)라고도 불린다.12

\(d_{L1}(p_1, p_2) = |x_1-x_2| + |y_1-y_2|\) 맨해튼 거리의 가장 큰 장점은 계산의 단순함에 있다. 제곱근 연산이 필요한 유클리드 거리와 달리, 맨해튼 거리는 뺄셈과 덧셈만으로 계산이 가능하여 계산 비용이 매우 저렴하다. 이 때문에 실시간 성능이 극도로 중요한 일부 복셀 렌더링과 같은 응용에서는 정확도를 일부 희생하고 맨해튼 거리를 사용한 SDF를 근사치로 사용하기도 한다.7

메트릭 선택의 의미

거리 메트릭의 선택은 단순히 계산 방식의 차이를 넘어, 생성되는 거리 필드의 형태와 응용의 적합성에 근본적인 영향을 미친다. 이는 ‘정확성’과 ‘계산 효율성’ 사이의 고전적인 공학적 트레이드오프를 명확하게 보여준다.

기하학적 형상을 가장 충실하게 표현하는 것이 목표라면, 최단 거리를 나타내는 유클리드 거리가 당연히 표준이 되어야 한다. 하지만 실시간 시스템에서는 매 프레임마다 수백만 개의 복셀에 대해 거리 계산을 수행해야 할 수 있으며, 이때 유클리드 거리의 제곱근 연산은 상당한 계산 부하를 유발할 수 있다. 반면, 맨해튼 거리는 훨씬 빠른 계산 속도를 제공한다.

이러한 선택의 결과는 생성되는 SDF의 등고선(iso-contours)에서 명확하게 드러난다. 유클리드 거리 기반 SDF의 등고선은 점 소스(point source)로부터 원형(3D에서는 구형)으로 퍼져나가는 반면, 맨해튼 거리 기반 SDF의 등고선은 마름모 또는 정사각형(3D에서는 정팔면체) 형태로 나타난다.16 따라서, 응용 프로그램이 요구하는 기하학적 정확도 수준과 가용한 계산 자원을 신중하게 고려하여 적절한 거리 메트릭을 선택해야 한다. ‘ESDF’라는 용어는 암묵적으로 유클리드 거리를 가정하지만, 실제 구현에서는 성능 최적화를 위해 다른 메트릭이 사용될 수 있음을 항상 인지하고 있어야 한다.

ESDF를 계산하는 과정은 주어진 기하학적 표현(예: 이진 점유 격자, 다각형 메시)으로부터 공간의 각 지점까지의 최단 거리를 찾는 것으로, 이를 효율적으로 수행하기 위한 다양한 알고리즘이 개발되었다. 이 알고리즘들은 크게 환경이 변하지 않는다고 가정하고 한 번에 전체 필드를 계산하는 ‘배치(batch) 기법’과, 환경이 실시간으로 변하는 상황에 대응하여 변경된 부분만 업데이트하는 ‘점진적(incremental) 기법’으로 나눌 수 있다.

배치 기법은 주로 오프라인 환경에서 고정된 객체나 장면에 대한 ESDF를 생성할 때 사용된다. 가장 일반적인 출발점은 공간을 이산적인 복셀(voxel) 그리드로 나누고, 각 복셀이 장애물에 의해 ‘점유(occupied)’되었는지 혹은 ‘비어(free)’있는지를 나타내는 이진 점유 격자 지도(occupancy grid map)이다.10

거리 변환(Distance Transform, DT)

거리 변환은 이진 입력(예: 0과 1, 또는 true와 false)을 가진 그리드의 각 셀에 대해, ‘참(true)’ 또는 ‘점유’ 상태인 가장 가까운 셀까지의 거리를 계산하여 새로운 그리드를 생성하는 연산이다.10 ESDF를 생성하기 위해, 점유된 셀들을 ‘참’으로 간주하여 DT를 한 번 수행하고(내부 거리 필드), 비어있는 셀들을 ‘참’으로 간주하여 DT를 또 한 번 수행한 후(외부 거리 필드), 두 결과를 조합하여 부호를 부여하는 방식을 사용할 수 있다.10

Marching Parabolas 알고리즘 심층 분석

CPU 환경에서 매우 효율적인 ESDF 생성 알고리즘으로 Pedro Felzenszwalb와 Daniel Huttenlocher가 제안한 ‘Marching Parabolas’가 있다. 이 알고리즘은 그리드 크기 N에 대해 선형 시간(O(N))의 계산 복잡도를 가지므로 대규모 그리드에서도 빠른 성능을 보인다.10

이 알고리즘의 핵심 아이디어는 두 가지다. 첫째, 2차원 거리 변환을 두 개의 독립적인 1차원 거리 변환으로 분리(separable)하는 것이다. 이는 2D 이미지 필터를 가로 방향 패스와 세로 방향 패스로 나누어 적용하는 것과 유사하다. 이를 위해 먼저 이진 입력 그리드의 ‘점유’ 셀은 0으로, ‘비어있는’ 셀은 무한대(∞)로 초기화한다.10

둘째, 1차원 제곱 유클리드 거리 변환(Squared Euclidean Distance Transform, SEDT) 문제를 기하학적으로 재해석하는 것이다. 1차원 그리드의 각 점 i를 꼭짓점이 $(i, g(i))$에 위치한 표준 2차 포물선 $p_i(x) = (x-i)^2 + g(i)$으로 간주할 수 있다. 여기서 $g(i)$는 초기 그리드의 값(0 또는 ∞)이다. 그러면 1차원 SEDT는 이 포물선들의 집합에 대한 하위 포락선(lower envelope), 즉 아래쪽 경계선을 찾는 문제와 동일해진다.10

Marching Parabolas 알고리즘은 다음 단계로 수행된다 10:

1. 포물선 해석: 입력 이미지의 각 행(row)에 대해, 0 값을 가진 픽셀을 꼭짓점으로 하는 포물선들의 집합을 생성한다.
2. 하위 볼록 껍질 탐색 (find_hull_parabolas): 왼쪽에서 오른쪽으로 스캔하면서 포물선들을 순차적으로 추가한다. 새로운 포물선이 기존의 하위 껍질을 형성하던 포물선을 완전히 가리게 되면(occlude), 기존 포물선을 제거한다. 이 과정을 통해 최종적으로 하위 포락선을 구성하는 포물선들의 목록과 그들의 교차점을 찾는다.
3. 거리 값 샘플링 (march_parabolas): 결정된 하위 껍질을 따라 다시 왼쪽에서 오른쪽으로 이동하며, 각 픽셀 위치에서 현재 구간에 해당하는 포물선의 y값(제곱 거리)을 계산하여 저장한다.
4. 전치 및 반복: 이미지 전체를 전치(transpose)시킨 후, 모든 열에 대해 1~3단계를 반복한다. 최종적으로 얻어진 SEDT 값에 제곱근을 취하면 EDT(Euclidean Distance Transform)가 완성된다.

GPU 가속 기법

대규모 병렬 처리가 가능한 GPU의 발달로, ESDF 생성을 가속화하는 다양한 기법들이 제안되었다.

• Scan Conversion: 다각형 메시로 표현된 객체의 각 기하학적 프리미티브(점, 선, 삼각형)를 감싸는 경계 볼륨(bounded volume)을 생성하고, 이 볼륨을 GPU로 래스터화(scan-convert)한다. 그리고 각 복셀(프래그먼트)에 대해 해당 프리미티브까지의 최단 거리를 프래그먼트 셰이더에서 계산하는 방식이다.1
• Jump Flooding Algorithm (JFA): GPU 병렬 처리에 매우 적합한 근사 알고리즘이다. 초기에는 각 ‘점유’ 픽셀만 자신의 위치를 ‘가장 가까운 점’ 정보로 가진다. 이후 여러 패스에 걸쳐, 각 픽셀은 2k 거리만큼 떨어진 이웃 픽셀들과 정보를 교환하며 자신의 ‘가장 가까운 점’ 정보를 점진적으로 업데이트한다. 패스가 거듭될수록 정보가 기하급수적으로 전파되어 빠르게 수렴한다.

로봇이 미지의 환경을 탐색하거나, 환경 내에 움직이는 장애물이 있는 동적 시나리오에서는 매 순간 센서 정보가 갱신된다. 이러한 상황에서 매번 전체 맵에 대해 배치 알고리즘을 실행하는 것은 극심한 계산 낭비이다. 따라서 변경된 부분만 효율적으로 업데이트하는 점진적(incremental) 방식이 필수적이다.20

Voxblox: TSDF로부터 ESDF 점진적 구축

로보틱스 분야에서 널리 사용되는 점진적 ESDF 생성 프레임워크로 ‘Voxblox’가 있다.23 Voxblox의 핵심 전략은 센서 데이터를 직접 ESDF로 변환하는 것이 아니라, 중간 표현으로 TSDF(Truncated Signed Distance Field)를 사용하는 것이다.20

이러한 TSDF-ESDF 파이프라인은 ‘센서 데이터의 물리적 특성’과 ‘응용 프로그램의 요구사항’ 사이의 간극을 메우는 매우 실용적이고 영리한 공학적 해결책이다. 그 배경을 살펴보면 다음과 같다.

1. 센서의 현실: 로보틱스에서 널리 사용되는 깊이 카메라(RGB-D)는 센서 원점으로부터 발사된 광선(ray)을 따라 표면까지의 거리를 측정한다. 이는 진정한 3D 공간상의 최단 유클리드 거리가 아닌, ‘투영 거리(projective distance)’이다.25
2. TSDF의 역할: 이 투영 거리를 직접, 그리고 계산 효율성과 메모리 절약을 위해 표면 근처의 좁은 영역(truncation)에서만 저장하는 것이 TSDF의 핵심이다. 이는 깊이 센서 데이터를 실시간으로 빠르고 견고하게 융합(fusion)하여 3D 모델을 구축하는 데 매우 최적화된 표현 방식이다.20
3. 응용의 요구: 하지만 로봇의 경로 계획이나 충돌 회피와 같은 고수준 응용은 장애물까지의 실제 최단 거리, 즉 ‘유클리드 거리’와 그 그래디언트 정보를 필요로 한다.25
4. 해결책(파이프라인): 따라서 Voxblox와 같은 시스템은 이 두 요구사항을 모두 충족시키기 위해 분업 구조를 채택한다. 먼저, 들어오는 센서 데이터를 TSDF에 빠르게 통합하여 실시간으로 맵을 구축한다(1차 매핑). 그 다음, 이렇게 구축된 TSDF 맵에서 변경된 부분을 감지하고, 그 변경 사항을 기반으로 ESDF를 점진적으로 업데이트하여 플래너에게 제공한다.

이 업데이트 과정은 파면 전파(Wavefront Propagation) 원리를 기반으로 하며, 두 개의 우선순위 큐(priority queue)를 사용하여 효율적으로 관리된다.20

• lower 큐: 새로운 장애물이 관측되거나 기존 경로보다 더 짧은 경로가 발견되어 거리 값이 ‘작아져야’ 하는 복셀들을 관리한다. 이 큐의 복셀들은 주변 이웃들에게 더 짧은 거리 정보를 전파하는 파면의 시작점이 된다.
• raise 큐: 기존 장애물이 사라져 거리 값이 ‘커져야’ 하는 복셀들을 관리한다. 이 복셀에 의존하던 주변 복셀들은 이제 최단 거리 정보를 잃었으므로, 재계산이 필요함을 알리는 역할을 한다.

Voxblox의 점진적 업데이트 알고리즘은 다음과 같이 요약할 수 있다 20:

1. 변경 감지: 새로운 센서 데이터가 TSDF에 통합되면서 값이 변경된 복셀들을 식별한다.
2. 큐 삽입: 변경된 복셀의 이전 값과 새 값을 비교하여 raise 또는 lower 큐에 삽입한다.
3. raise 전파: 먼저 raise 큐를 처리한다. 큐에서 복셀을 꺼내 거리 값을 무한대로 설정하고, 이 복셀을 최단 거리 경로의 부모로 삼고 있던 이웃들을 재귀적으로 raise 큐에 추가한다. 이를 통해 유효하지 않게 된 거리 정보를 맵에서 제거한다.
4. lower 전파: raise 큐가 비워지면 lower 큐를 처리한다. 큐에서 복셀을 꺼내, 26-방향 이웃(3D 그리드에서 인접한 모든 복셀)을 확인한다. 만약 현재 복셀을 통해 이웃으로 가는 경로가 이웃의 기존 최단 거리보다 짧다면, 이웃의 거리 값을 갱신하고 lower 큐에 삽입한다. 이 과정이 큐가 빌 때까지 반복되면서 새로운 최단 거리 정보가 파도처럼 퍼져나간다.

이러한 점진적 방식은 전체 맵이 아닌, 변경이 발생한 국소적인 영역에만 계산을 집중함으로써 실시간 동적 환경에서의 ESDF 유지를 가능하게 한다.

알고리즘 (Algorithm)	계산 복잡도 (Complexity)	정확도 (Accuracy)	병렬성 (Parallelism)	입력 데이터 (Input Data)	주요 특징 (Key Features)	관련 자료
Marching Parabolas	O(N) (N=픽셀 수)	정확함 (Exact)	제한적 (행/열 단위)	이진 그리드	CPU 친화적, 분리 가능한 필터 원리	10
Fast Marching Method	O(NlogN)	근사/정확	제한적 (우선순위 큐)	이진 그리드	파면 전파 기반, 아이코날 방정식 풀이	7
Jump Flooding	O(logD) 패스 (D=최대 거리)	근사 (Approximation)	매우 높음 (Massively Parallel)	이진 그리드	GPU에 매우 적합, 간단한 구현	(일반적인 GPU 기법)
Scan Conversion	O(M⋅V) (M=프리미티브, V=복셀)	정확함 (Exact)	높음 (프리미티브 단위)	다각형 메시	GPU 가속, 좁은 밴드에서 작동	1
Voxblox (Incremental)	업데이트 영역에 비례	정확함 (TSDF 오차 제외)	중간 (멀티스레딩)	TSDF	점진적 업데이트, 동적 환경용	20

ESDF의 풍부한 기하학적 정보와 강력한 수학적 특성은 컴퓨터 그래픽스와 로보틱스 분야에서 다양한 문제들을 해결하는 핵심적인 도구로 활용되게 하였다.

컴퓨터 그래픽스 분야에서 ESDF는 전통적인 다각형 메시 기반의 렌더링 및 시뮬레이션 패러다임을 벗어나는 새로운 가능성을 열었다.

실시간 렌더링: 레이마칭 (Ray Marching)

레이마칭은 SDF로 정의된 암시적 표면을 렌더링하는 대표적인 기법이다.9 기존의 레이 트레이싱(ray tracing)이 광선과 객체의 교차점을 해석적으로 계산하는 반면, 레이마칭은 광선을 따라 일정한 간격으로 전진하며 표면을 찾아 나가는 방식이다.

이 과정에서 ESDF는 스피어 트레이싱(Sphere Tracing)이라는 최적화 기법을 통해 비약적인 효율성 향상을 가져온다. 그 원리는 다음과 같다 9:

1. 안전 거리 보장: 광선 상의 현재 위치 p에서 계산된 ESDF 값 $d = f(p)$는, 점 p를 중심으로 하고 반지름이 d인 구(sphere)가 장면의 어떤 표면과도 교차하지 않음을 보장한다. 즉, d는 표면과 충돌하지 않고 ‘안전하게 전진할 수 있는 최소 거리’이다.
2. 효율적인 전진: 따라서 광선은 매우 작은 고정된 스텝으로 전진하는 대신, 매 스텝마다 ESDF 값 d만큼 큰 보폭으로 전진할 수 있다.
3. 수렴: 광선이 표면에 가까워질수록 ESDF 값은 작아지고, 전진하는 거리도 점차 줄어든다. 이 과정을 반복하면 광선은 표면에 매우 효율적으로 수렴하게 된다. ESDF 값이 아주 작은 임계값(epsilon)보다 작아지면 표면에 도달했다고 판단한다.

이러한 레이마칭 기법은 복잡한 프랙탈(fractal) 구조, 무한히 반복되는 절차적(procedural) 형상, 또는 CSG(Constructive Solid Geometry) 연산으로 정의된 객체들을 다각형 메시로 변환하는 어려운 과정 없이 직접 렌더링할 수 있게 해준다.9

기타 응용

• 물리 기반 시뮬레이션: ESDF는 옷감 시뮬레이션, 유체 역학, 변형 가능한 객체 및 다물체 동역학 시뮬레이션에서 객체 간의 충돌 감지(collision detection) 및 거리 계산을 위해 매우 효과적으로 사용된다. 객체 표면까지의 거리를 빠르게 조회할 수 있어 복잡한 충돌 반응을 실시간으로 계산하는 데 유리하다.1
• 고품질 폰트 렌더링: 글꼴의 외곽선으로부터 생성된 2D SDF를 텍스처에 저장하면, 이 텍스처를 확대하거나 축소해도 픽셀 보간을 통해 항상 날카롭고 깨끗한 경계를 유지하는 고품질의 벡터 폰트 렌더링이 가능하다. 이는 저해상도 텍스처만으로도 해상도에 독립적인 렌더링을 가능하게 한다.10
• 절차적 텍스처 및 지형 생성: 여러 기본 도형의 SDF를 조합하고 변형하여 복잡한 절차적 패턴이나 지형을 생성하는 데 활용될 수 있다.10

로보틱스 분야에서 ESDF는 로봇이 주변 환경을 인식하고, 안전하게 움직이기 위한 계획을 수립하는 데 있어 핵심적인 역할을 수행한다.

경로 계획 및 충돌 회피

현대 로보틱스의 경로 계획(path planning)은 단순히 시작점에서 목표점까지의 경로를 찾는 것을 넘어, 경로의 부드러움, 에너지 효율성, 안전성 등을 모두 고려하는 최적화 문제로 발전했다. CHOMP, TrajOpt, GPMP2와 같은 최적화 기반 플래너들은 경로를 표현하는 수많은 점들에 대해 비용 함수(cost function)와 그 그래디언트(gradient)를 반복적으로 계산하여 경로를 점차 개선해 나간다.22

ESDF는 이러한 최적화 기반 플래너들에게 완벽한 기반을 제공한다.

• 충돌 비용 함수: 로봇의 특정 지점(예: 로봇 팔의 각 관절)에서 ESDF 값을 조회하면 가장 가까운 장애물까지의 거리를 즉시 알 수 있다. 이를 이용하여 거리가 특정 안전 마진(safety margin)보다 작아지면 비용이 급격히 증가하는 연속적인 충돌 비용 함수를 쉽게 정의할 수 있다.25
• 그래디언트 활용: ESDF의 가장 강력한 특징은 그 그래디언트 정보에 있다. ESDF의 그래디언트 ∇f는 ‘거리’라는 스칼라 필드를 ‘행동 방향’이라는 벡터 필드로 변환하는 다리 역할을 한다. 이는 로봇의 인식(perception)과 계획(planning)을 연결하는 핵심 메커니즘이다.
  1. 인식의 결과: 센서 데이터를 융합하여 로봇은 ESDF라는 환경 지도를 구축한다. 이 단계의 정보는 ‘A 지점에서 장애물까지의 거리는 dA이다’와 같은 수동적인 스칼라 정보다.20
  2. 계획의 질문: 로봇이 충돌 위험에 처했을 때, ‘어느 방향으로 움직여야 가장 안전한가?’라는 질문에 답하기 위해서는 방향, 즉 벡터 정보가 필요하다.
  3. 그래디언트의 역할: 미분 연산인 그래디언트는 스칼라 필드의 각 점에서 값이 가장 빠르게 증가하는 방향을 나타내는 벡터 필드를 유도한다. ESDF에서 ∇f는 거리가 가장 빠르게 증가하는 방향, 즉 장애물로부터 가장 효과적으로 멀어지는 방향을 가리킨다.7
  4. 실행 가능한 지침: CHOMP와 같은 플래너는 이 그래디언트 벡터를 직접 사용하여 경로 상의 점들을 충돌 영역 밖으로 ‘밀어내는(pushing)’ 방식으로 경로를 수정한다.22 따라서 ESDF는 단순한 거리 맵이 아니라, 로봇에게 ‘어디로 가야 하는지’에 대한 명확하고 실행 가능한 지침을 제공하는 능동적인 정보 소스가 된다.

SLAM (Simultaneous Localization and Mapping)

SLAM은 로봇이 미지의 환경을 탐색하면서 자신의 위치를 추정하고 동시에 지도를 작성하는 기술이다. 2D-SDF-SLAM과 같은 연구에서는 기존의 점유 격자 지도 대신 SDF를 맵 표현으로 사용하여, 복셀 크기보다 더 높은 아-복셀(sub-voxel) 정밀도로 환경을 모델링할 수 있음을 보였다. 이를 통해 로봇의 위치 추정 정확도를 크게 향상시켰다.19 또한, SDF의 미분 가능성 덕분에 스캔 정합(scan matching) 과정에서 Gauss-Newton과 같은 효율적인 비선형 최적화 기법을 직접 적용할 수 있어, 기존의 브루트포스 방식보다 더 빠르고 정확한 정합이 가능하다.

로봇 및 환경 모델링

ESDF는 외부 환경뿐만 아니라 로봇 자체의 기하학적 구조를 표현하는 데에도 사용될 수 있다. 로봇의 각 링크(link)를 개별적인 SDF로 모델링하고, 이를 로봇의 관절 각도(joint angles)에 따라 실시간으로 변환 및 합성하면, 로봇의 자기 충돌(self-collision)이나 복잡한 환경과의 상호작용을 매우 효율적으로 검사할 수 있다.11 또한, CBF(Control Barrier Function)와 같은 안전 보장 제어 기법에서는, 복잡한 형태의 수많은 장애물들을 ESDF라는 단일 연속 함수로 표현하여 안전 제약 조건을 단순화하고 실시간 제어기 설계에 활용할 수 있다.28

ESDF는 그 자체로도 강력한 표현 방식이지만, 그 가치와 특성은 다른 유사한 표현 방식과의 비교를 통해 더욱 명확해진다. 특히 로보틱스 분야에서 ESDF와 함께 자주 언급되는 TSDF와의 차이점을 이해하고, 최근 3D 딥러닝 분야에서 등장한 신경망 기반 SDF의 혁신을 살펴보는 것은 매우 중요하다.

ESDF와 TSDF는 둘 다 부호화된 거리 필드라는 점에서 공통점을 가지지만, 거리 측정 방식과 데이터 저장 전략에서 결정적인 차이를 보인다.

핵심 차이점

• 거리 메트릭 (Distance Metric): 가장 근본적인 차이는 거리 측정 방식에 있다. ESDF는 이름 그대로 공간상의 두 점을 잇는 최단 직선 거리인 진정한 유클리드 거리(true Euclidean distance)를 저장한다.25 반면, TSDF는 주로 깊이 카메라와 같은 센서로부터 실시간으로 생성되는데, 이때 저장되는 거리는 센서의 광학 중심에서 나온 광선(ray)을 따라 측정된 투영 거리(projective distance)이다.24 이 투영 거리는 센서를 정면으로 바라보는 평평한 표면에서는 유클리드 거리와 유사하지만, 표면이 곡면이거나 센서의 시야각 가장자리에 위치할 경우 실제 최단 거리와 상당한 오차를 보일 수 있다.20
• 절단 (Truncation): TSDF는 이름(Truncated)에서 알 수 있듯이, 표면 주변의 좁은 밴드(narrow band) 내에서만 유효한 거리 값을 저장하고, 그 밴드 밖의 영역은 일정한 최대/최소 값으로 잘라낸다(truncate). 이는 두 가지 주요 목적을 가진다. 첫째, 대부분의 공간을 차지하는 빈 공간(free space)에 대한 정보를 저장하지 않음으로써 메모리 사용량을 크게 절약한다. 둘째, 투영 거리의 오차가 표면에서 멀리 떨어진 곳까지 영향을 미치는 것을 방지한다.25 반면, ESDF는 원칙적으로 공간의 모든 점에 대해 유효한 거리 값을 정의한다.

트레이드오프와 사용 시나리오

이러한 차이점들은 각 표현 방식이 특정 응용에 더 적합하게 만드는 트레이드오프로 이어진다.

• TSDF는 깊이 센서 데이터를 실시간으로 융합하여 3D 표면을 재구성하는 작업(real-time surface reconstruction)에 매우 최적화되어 있다. Microsoft의 KinectFusion이 이 기술을 대중화시킨 대표적인 예이다.25 계산이 빠르고 센서 노이즈에 강건하여, 로봇이 움직이면서 주변 환경을 매핑하는 데 널리 사용된다.
• ESDF는 경로 계획, 충돌 비용 계산, 동역학 시뮬레이션 등 정확한 최단 거리와 그 그래디언트 정보가 필수적인 고수준 응용에 사용된다.22
• 결합 사용: 앞서 ‘Voxblox’ 사례에서 살펴보았듯이, 현대의 실시간 로보틱스 시스템은 이 두 표현 방식의 장점을 모두 취하는 하이브리드 접근법을 채택하는 경우가 많다. 먼저 TSDF를 사용하여 센서 데이터를 빠르게 융합해 1차적인 맵을 생성하고(Mapping), 이렇게 생성된 TSDF를 기반으로 경로 계획에 필요한 ESDF를 점진적으로 구축(Planning)하는 것이다.20

특성 (Characteristic)	Euclidean Signed Distance Field (ESDF)	Truncated Signed Distance Field (TSDF)
거리 메트릭	실제 유클리드 거리 (True Euclidean)	센서 광선 기준 투영 거리 (Projective)
정확도	높음, 기하학적으로 정확함	근사치, 곡면에서 오차 발생 가능
절단 (Truncation)	없음 (원칙적)	있음 (표면 주변 좁은 밴드)
주요 생성원	점유 그리드, TSDF, 메시	깊이 센서 데이터 (RGB-D)
계산 효율성	상대적으로 높음 (배치 기준)	매우 높음 (실시간 융합)
메모리 사용량	높음 (절단 없을 시)	낮음 (절단으로 인해)
주요 응용 분야	경로 계획, 충돌 회피, 최적화	실시간 3D 재구성, SLAM 매핑
관련 자료	22	20

최근 몇 년간 3D 비전 및 그래픽스 분야는 딥러닝 기술의 도입으로 급격한 변화를 겪고 있으며, SDF 표현 방식 역시 예외는 아니다. 신경망을 이용한 새로운 SDF 패러다임이 등장하며 기존 방식의 한계를 극복하고 새로운 가능성을 열고 있다.

기존 그리드 기반 SDF의 한계

고전적인 ESDF/TSDF는 복셀 그리드(voxel grid)라는 이산적인 데이터 구조에 기반한다. 이는 다음과 같은 근본적인 한계를 가진다.

• 이산성 및 메모리 문제: 표현의 정밀도가 복셀의 크기에 의해 제한되며, 고해상도를 얻기 위해서는 복셀의 수를 늘려야 한다. 이 경우 메모리 사용량은 해상도의 세제곱에 비례하여 기하급수적으로 증가한다 (O(N3)).4
• 표현 범위의 제한: 그리드 기반 SDF는 특정 3D 모델이나 스캔된 장면 하나, 즉 단일 인스턴스(instance)의 기하학적 정보만을 표현할 수 있다. ‘의자’라는 일반적인 개념을 표현할 수는 없고, ‘특정한 하나의 의자 모델’만을 표현할 뿐이다.4

DeepSDF의 혁신

2019년에 발표된 DeepSDF는 이러한 한계를 극복하기 위해 신경망, 특히 다층 퍼셉트론(Multi-Layer Perceptron, MLP)을 사용하여 SDF를 표현하는 혁신적인 방법을 제안했다.2 DeepSDF의 등장은 3D 기하학을 다루는 방식에 있어 근본적인 패러다임 전환을 의미한다. 이는 3D 기하학을 단순히 ‘측정하고 재구성하는(measuring and reconstructing)’ 대상에서 ‘이해하고 생성하며 편집하는(understanding, generating, and editing)’ 대상으로 바꾸었기 때문이다.

1. 전통적 접근: 고전적 ESDF/TSDF 생성의 목표는 주어진 센서 데이터로부터 특정 인스턴스의 기하학적 구조를 최대한 충실하게 복원하는 것이었다.6
2. DeepSDF의 질문: DeepSDF는 ‘의자란 무엇인가?’와 같은 더 근본적인 질문을 던진다. 즉, 개별적인 의자 메시들을 넘어 ‘의자다움’이라는 추상적인 개념 자체를 학습할 수 있는지를 탐구한다.
3. 잠재 공간의 역할: DeepSDF는 잠재 공간(latent space)이라는 저차원 벡터 공간을 도입하여 이 질문에 답한다. 잠재 공간의 각 점(잠재 벡터 z)은 유효한 ‘의자’ 형상 하나에 대응한다. 이 공간 내에서 두 점 사이를 보간(interpolation)하면, 하나의 의자 형태가 다른 의자 형태로 자연스럽게 변형되는 것을 관찰할 수 있다.4 이는 네트워크가 단순히 수많은 형상을 암기한 것이 아니라, 해당 형상 클래스의 기저에 있는 ‘형상 매니폴드(shape manifold)’를 학습했음을 시사한다.
4. 새로운 능력의 발현: 이 강력한 잠재 공간 덕분에, 이전에는 불가능했던 새로운 작업들이 가능해진다. 예를 들어, 부분적인 포인트 클라우드만 보고도 전체 형상을 ‘상상’하여 복원하는 형상 완성(shape completion), 또는 이전에 본 적 없는 새로운 디자인의 의자를 ‘창조’하는 형상 생성(shape generation)이 가능해진다.
5. 패러다임 전환: 결과적으로, 3D 모델링은 정적인 재구성 작업에서 동적인 생성 및 조작 작업으로 격상된다. 형상은 더 이상 고정된 데이터가 아니라, 조작 가능한 잠재 벡터에 의해 제어되는 유연하고 연속적인 표현이 된다.

DeepSDF의 핵심적인 기술적 특징은 다음과 같다 5:

• 연속적 표현: 신경망 MLP를 사용하여 3D 좌표 x와 잠재 벡터 z를 입력으로 받아 해당 지점의 SDF 값을 출력하는 연속 함수 $f_\theta(z, x)$를 학습한다. 이로써 복셀 그리드가 필요 없어져 메모리 문제를 해결하고, 임의의 해상도로 정밀한 표면을 추출할 수 있다.
• 클래스 표현과 잠재 벡터: 잠재 벡터 z는 특정 형상의 ‘정체성’을 인코딩하는 압축된 코드 역할을 한다. 하나의 신경망 fθ는 ‘의자’, ‘비행기’ 등 특정 ‘클래스’에 속하는 형상들의 공통적인 구조를 학습하고, 개별 인스턴스는 각기 다른 z 값으로 구분되어 표현된다.
• Auto-Decoder 구조: DeepSDF는 일반적인 Auto-Encoder와 달리 인코더(Encoder) 없이 디코더(Decoder, SDF 생성 네트워크)만으로 구성된다. 학습 시에는 각 훈련 형상에 해당하는 잠재 벡터 z를 네트워크 가중치 θ와 함께 공동으로 최적화한다. 추론 시(예: 형상 완성)에는, 주어진 부분 데이터에 대해 SDF 손실을 최소화하는 최적의 잠재 벡터 z를 경사 하강법으로 찾아내어 전체 형상을 복원한다.

최신 연구 동향

DeepSDF 이후, 신경망 기반 SDF 연구는 더욱 활발해지고 있다.

• Curriculum DeepSDF: 사람이 쉬운 개념부터 배우고 점차 어려운 개념으로 나아가는 것처럼, 학습 과정을 설계하여 성능을 향상시킨다. 처음에는 전체적인 형상(coarse shape)을 학습하게 하고, 점차 복잡하고 세밀한 국소적 디테일에 집중하도록 학습 난이도를 조절한다.32
• Diffusion-SDF: 최근 이미지 생성 분야에서 큰 성공을 거둔 확산 모델(diffusion model)을 3D SDF 생성에 적용한 연구이다. 가우시안 노이즈 상태에서 시작하여, 점진적으로 노이즈를 제거하는 역방향 프로세스를 학습함으로써 고품질의 다양한 3D 형상을 생성하는 생성 모델을 제안한다.8

기준 (Criterion)	고전적 SDF (ESDF/TSDF)	신경망 SDF (예: DeepSDF)
표현 방식	이산적 (Discrete, Voxel Grid)	연속적 (Continuous, MLP)
표현 대상	단일 인스턴스 (Single Instance)	형상 클래스 (Class of Shapes)
메모리	해상도에 비례 (고)	네트워크 파라미터 수에 비례 (저)
주요 기능	3D 재구성 (Reconstruction)	재구성, 생성(Generation), 보간(Interpolation), 완성(Completion)
일반화 능력	없음	높음 (학습된 클래스 내에서)
데이터 요구사항	3D 스캔 데이터 (메시, 포인트 클라우드)	대규모 3D 형상 데이터셋
핵심 기술	거리 변환, 파면 전파	심층 학습 (Auto-Decoder, Latent Vector)
관련 자료	10	4

본 보고서를 통해 유클리드 부호 거리 필드(ESDF)가 단순한 거리 정보를 담은 데이터 구조를 넘어, 풍부한 기하학적 정보를 내포한 강력한 암시적 표면 표현 방식임을 확인하였다. ESDF의 핵심 가치는 그 연속성과 미분 가능성에 있다. 이 두 가지 특성은 ESDF가 단순한 점유 여부를 넘어, 표면까지의 정확한 거리와 표면의 방향(법선 벡터) 정보를 공간 전체에 걸쳐 제공하게 만든다.

이러한 특성 덕분에 ESDF는 다양한 분야에서 근본적인 문제 해결 도구로 자리매김했다. 컴퓨터 그래픽스에서는 레이마칭과 같은 효율적인 실시간 렌더링 기법을 가능하게 했고, 물리 시뮬레이션에서는 정밀한 충돌 감지의 기반이 되었다. 특히 로보틱스 분야에서 ESDF의 가치는 더욱 두드러진다. 최적화 기반 경로 계획 알고리즘에 필수적인 연속적인 비용 함수와 그래디언트를 제공함으로써, 로봇이 복잡하고 동적인 환경에서도 안전하고 효율적으로 움직일 수 있는 길을 열었다. ESDF의 그래디언트가 인식(perception)과 계획(planning) 사이의 간극을 메우는 핵심적인 역할을 수행한 것이다.

ESDF와 그 파생 기술들은 앞으로도 계속해서 발전하며 새로운 가능성을 탐색할 것으로 전망된다.

• 하이브리드 표현의 발전: 고전적인 ESDF가 가진 기하학적 정밀성과 실시간 계산 능력, 그리고 신경망 기반 SDF가 가진 강력한 일반화 및 생성 능력을 결합하는 하이브리드 접근법이 더욱 활발히 연구될 것이다. 예를 들어, 신경망이 전체적인 장면의 SDF를 대략적으로 생성하면, 이를 초기값으로 삼아 고전적인 점진적 업데이트 알고리즘이 실시간 센서 데이터에 맞춰 국소적인 영역을 정밀하게 수정하는 방식이 가능하다. 이는 두 패러다임의 장점을 모두 취하는 효과적인 해결책이 될 수 있다.
• 동적 및 시변(Time-varying) 환경으로의 확장: 현재 대부분의 신경망 SDF 연구는 정적인 객체나 장면에 초점을 맞추고 있다. 미래의 중요한 연구 방향은 이를 동적으로 변형되거나 움직이는 객체, 나아가 시간에 따라 변화하는 전체 장면에 적용하는 것이 될 것이다. 시간에 따른 변화까지 잠재 공간에 인코딩하여 4D 시공간을 표현하고 예측하는 연구는 자율주행차나 동적 환경에서의 로봇 상호작용에 혁신을 가져올 잠재력을 지닌다.
• 의미론적 이해와의 결합: ESDF가 ‘어디에’ 장애물이 있는지를 알려준다면, 미래의 표현 방식은 ‘그것이 무엇인지’까지 이해해야 한다. 신경망 기반 SDF를 의미론적 분할(semantic segmentation)이나 객체 인식과 결합하여, ‘피해야 할 벽’과 ‘상호작용 가능한 문’을 구분하는 등, 기하학적 정보를 넘어 의미론적 정보를 포함하는 ‘Semantic SDF’로의 발전이 기대된다.

결론적으로, ESDF는 앞으로도 로보틱스의 실시간 제어 및 계획 분야에서 그 중요성을 유지할 것이다. 동시에, DeepSDF로 시작된 신경망 기반의 접근법은 3D 데이터를 이해하고 생성하는 방식에 근본적인 변화를 가져오며, 고수준의 의미론적 이해와 결합하여 더욱 지능적인 3D 인식 및 상호작용의 새로운 시대를 열 것으로 전망된다.

1. Chapter 34. Signed Distance Fields Using Single-Pass GPU Scan Conversion of Tetrahedra, accessed July 31, 2025, https://developer.nvidia.com/gpugems/gpugems3/part-v-physics-simulation/chapter-34-signed-distance-fields-using-single-pass-gpu
2. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation, accessed July 31, 2025, https://arxiv.org/abs/1901.05103
3. 3D Reconstruction Based on Iterative Optimization of Moving Least-Squares Function, accessed July 31, 2025, https://www.mdpi.com/1999-4893/17/6/263
4. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation - CVF Open Access, accessed July 31, 2025, https://openaccess.thecvf.com/content_CVPR_2019/papers/Park_DeepSDF_Learning_Continuous_Signed_Distance_Functions_for_Shape_Representation_CVPR_2019_paper.pdf
5. [1901.05103] DeepSDF: Learning Continuous Signed Distance …, accessed July 31, 2025, https://ar5iv.labs.arxiv.org/html/1901.05103
6. A Survey of Surface Reconstruction from Point Clouds - Matthew Berger, accessed July 31, 2025, https://matthewberger.github.io/papers/reconsurvey.pdf
7. Signed distance function - Wikipedia, accessed July 31, 2025, https://en.wikipedia.org/wiki/Signed_distance_function
8. Diffusion-SDF: Conditional Generative Modeling of Signed Distance Functions - Princeton Computational Imaging Lab, accessed July 31, 2025, https://light.princeton.edu/wp-content/uploads/2023/10/diffsdf.pdf
9. Ray Marching and Signed Distance Functions - Jamie Wong, accessed July 31, 2025, https://jamie-wong.com/2016/07/15/ray-marching-signed-distance-functions/
10. Distance Fields, accessed July 31, 2025, https://prideout.net/blog/distance_fields/
11. Representing Robot Geometry as Distance Fields: Applications to Whole-body Manipulation - Idiap Publications, accessed July 31, 2025, https://publications.idiap.ch/attachments/papers/2024/Li_ICRA-2_2024.pdf

12. Difference Between L1/Manhattan and L2/Euclidean Distance

    by DataScienceSphere, accessed July 31, 2025, https://medium.com/@datasciencejourney100_83560/difference-between-l1-manhattan-and-l2-euclidean-distance-c70b5da25fe0

13. What is the difference between Euclidean distance and Manhattan distance?, accessed July 31, 2025, https://cambridgeinfotech.io/ufaq/what-is-the-difference-between-euclidean-distance-and-manhattan-distance/

14. Computing the Signed Distance Field

    by TKMI-kyon - Medium, accessed July 31, 2025, https://tkmikyon.medium.com/computing-the-signed-distance-field-a1fa9ba2fc7d

15. Analysis of euclidean distance and manhattan distance measure in face recognition, accessed July 31, 2025, https://www.researchgate.net/publication/293815690_Analysis_of_euclidean_distance_and_manhattan_distance_measure_in_face_recognition
16. Manhattan distance vs Euclidean distance - Mathematics Stack Exchange, accessed July 31, 2025, https://math.stackexchange.com/questions/1168759/manhattan-distance-vs-euclidean-distance
17. Why doesn’t the Manhattan distance approximate the Euclidean Distance as the city-block shrinks? : r/math - Reddit, accessed July 31, 2025, https://www.reddit.com/r/math/comments/1iesw9g/why_doesnt_the_manhattan_distance_approximate_the/
18. Occupancy grid to mesh : r/VoxelGameDev - Reddit, accessed July 31, 2025, https://www.reddit.com/r/VoxelGameDev/comments/190qbox/occupancy_grid_to_mesh/
19. (PDF) 2D-SDF-SLAM: A signed distance function based SLAM frontend for laser scanners, accessed July 31, 2025, https://www.researchgate.net/publication/308298063_2D-SDF-SLAM_A_signed_distance_function_based_SLAM_frontend_for_laser_scanners
20. Voxblox: Incremental 3D Euclidean Signed Distance Fields for On-Board MAV Planning - Helen Oleynikova, accessed July 31, 2025, https://helenol.github.io/publications/iros_2017_voxblox.pdf
21. Predicted Composite Signed-Distance Fields for Real-Time Motion Planning in Dynamic Environments - Ioannis Havoutis, accessed July 31, 2025, https://ihavoutis.github.io/publications/2021/ICAPS2021_Finean.pdf
22. Predicted Composite Signed-Distance Fields for Real-Time Motion Planning in Dynamic Environments - AAAI, accessed July 31, 2025, https://cdn.aaai.org/ojs/16010/16010-40-19503-1-2-20210517.pdf
23. Voxblox - voxblox documentation, accessed July 31, 2025, https://voxblox.readthedocs.io/en/latest/
24. Voxblox: Incremental 3D Euclidean Signed Distance Fields for On-Board MAV Planning, accessed July 31, 2025, https://huggingface.co/papers/1611.03631
25. Signed Distance Fields: A Natural Representation for Both Mapping …, accessed July 31, 2025, https://www.research-collection.ethz.ch/bitstream/handle/20.500.11850/128029/eth-50477-01.pdf
26. Voxfield: Non-Projective Signed Distance Fields for Online Planning and 3D Reconstruction, accessed July 31, 2025, https://www.ipb.uni-bonn.de/wp-content/papercite-data/pdf/pan2022iros.pdf
27. Truncated Signed Distance Fields Applied To Robotics - DiVA portal, accessed July 31, 2025, https://www.diva-portal.org/smash/get/diva2:1136113/FULLTEXT01.pdf
28. Safe Control using Occupancy Grid Map-based Control Barrier Function (OGM-CBF) - arXiv, accessed July 31, 2025, https://arxiv.org/html/2405.10703v1
29. nvblox: GPU-Accelerated Incremental Signed Distance Field Mapping - arXiv, accessed July 31, 2025, https://arxiv.org/html/2311.00626v2
30. Voxblox system diagram, showing how the TSDF and ESDF layers are… - ResearchGate, accessed July 31, 2025, https://www.researchgate.net/figure/Voxblox-system-diagram-showing-how-the-TSDF-and-ESDF-layers-are-interconnected-through_fig4_340459923

31. Open3D: How does volumetric integration work?

    by Aashutosh …, accessed July 31, 2025, https://aashutosh-py.medium.com/open3d-how-does-volumetric-integration-work-b41d3c14d4e6

32. Curriculum DeepSDF - Yueqi Duan, accessed July 31, 2025, https://duanyueqi.github.io/ECCV20_Curriculum%20DeepSDF.pdf
33. Diffusion-Based Signed Distance Fields for 3D Shape Generation - CVF Open Access, accessed July 31, 2025, https://openaccess.thecvf.com/content/CVPR2023/papers/Shim_Diffusion-Based_Signed_Distance_Fields_for_3D_Shape_Generation_CVPR_2023_paper.pdf